Arbres
D'après les supports de Didier Müller
Introduction
On appelle arbre tout graphe connexe sans cycle. Un graphe sans cycle mais non connexe est appelé une forêt. Une feuille ou sommet pendant est un sommet de degré 1.
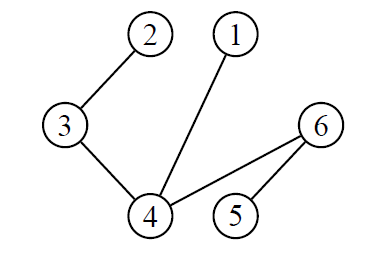
Théorème
Les affirmations suivantes sont équivalentes pour tout graphe G à n sommets
- G est un arbre
- G est sans cycle et connexe
- G est sans cycle et comporte n−1 arêtes
- G est connexe et comporte n−1 arêtes
- chaque paire u, v de sommets distincts est reliée par une seule chaîne simple (et le graphe est sans boucle)
Théorème
Tout arbre fini avec au moins deux sommets comporte au moins deux sommets pendants.
Arbre couvrant
Un arbre couvrant (aussi appelé arbre maximal) est un graphe partiel qui est aussi un arbre.

Algorithme de Kruskal
Soit le graphe G = (V,E) avec un poids associé à chacune de ses arêtes. On veut trouver, dans G, un arbre maximal A = (V,F) de poids total minimum.
L'algorithme de Kruskal propose une méthode qui revient à considérer les arêtes d'un graphe dans l'ordre croissant de leur poids et à les ajouter pour former l'arbre couvrant tant que tout le graphe n'est pas couvert et si les arêtes ainsi placées ne forment pas de cycle.

Arbre binaire de recherche
Un arbre binaire de recherche est un type d'arbre odronné particulier tel que :
- - Chaque noeud de l'arbre possède au plus 2 noeuds adjacents.
- - On hiérarchise l'arbre en parlant de père et de fils (on parlera de fils droit et de fils gauche).
On crée ainsi un arbre binaire. Un arbre binaire de recherche est une structure d'arbre binaire qui ajoute les contraintes suivantes :
- - Chaque noeuds possède une valeur qui l'identifie
- - Un père possède nécessairement une valeur plus grande que son fils gauche et plus petite que son fils droit