Bureau d'étude PEIP - ISs

L'algorithme des K-means

L'agorithme K-means est un algorithme de partitionnement de données ("clustering" en anglais), c'est à dire qu'il est capable d'identifier différents goupes homogènes de données au sein d'un ensemble hétérogène. Pour le dire autrement, étant données un paquet de données, l'algorithme sera capable le partitionner en "sous paquets" contenant des données qui semblent aller ensemble. C'est exactement comme si on vous donnez un sac de bille et que vous triez les billes pour faire des tas par couleur.

Prenons le cas plus abstrait d'un nuage de point. Si vous regardez la figure ci-dessous (source : Wikipédia), il apparaît assez nettement que 4 groupes distincts de points sont présents.

Le fonctionnement général de l'agoritgme K-means est le suivant : considérant un nuage de point et sachant qu'on doit former "k" groupes (dans notre exemple k=4), on commence par choisir 4 points au hasard dans l'espace (pas forcément des points du nuage, juste des points complétement aléatoires). Ces points sont appelés "centroïdes". Pour chaque point du nuage, on le place dans le même groupe que la centroïde dont il est le plus proche. Cela nous donne donc k groupes (un par centroïde). On calcul ensuite le barycentre de chacun de ces groupes, et les barycentres deviennent les nouvelles centroïdes. On recommence ainsi jusqu'à ce que les groupes ne bougent plus.

Reprennons notre exemple précédent : on tire 4 centroïdes au hasard (étape d'initialisation):

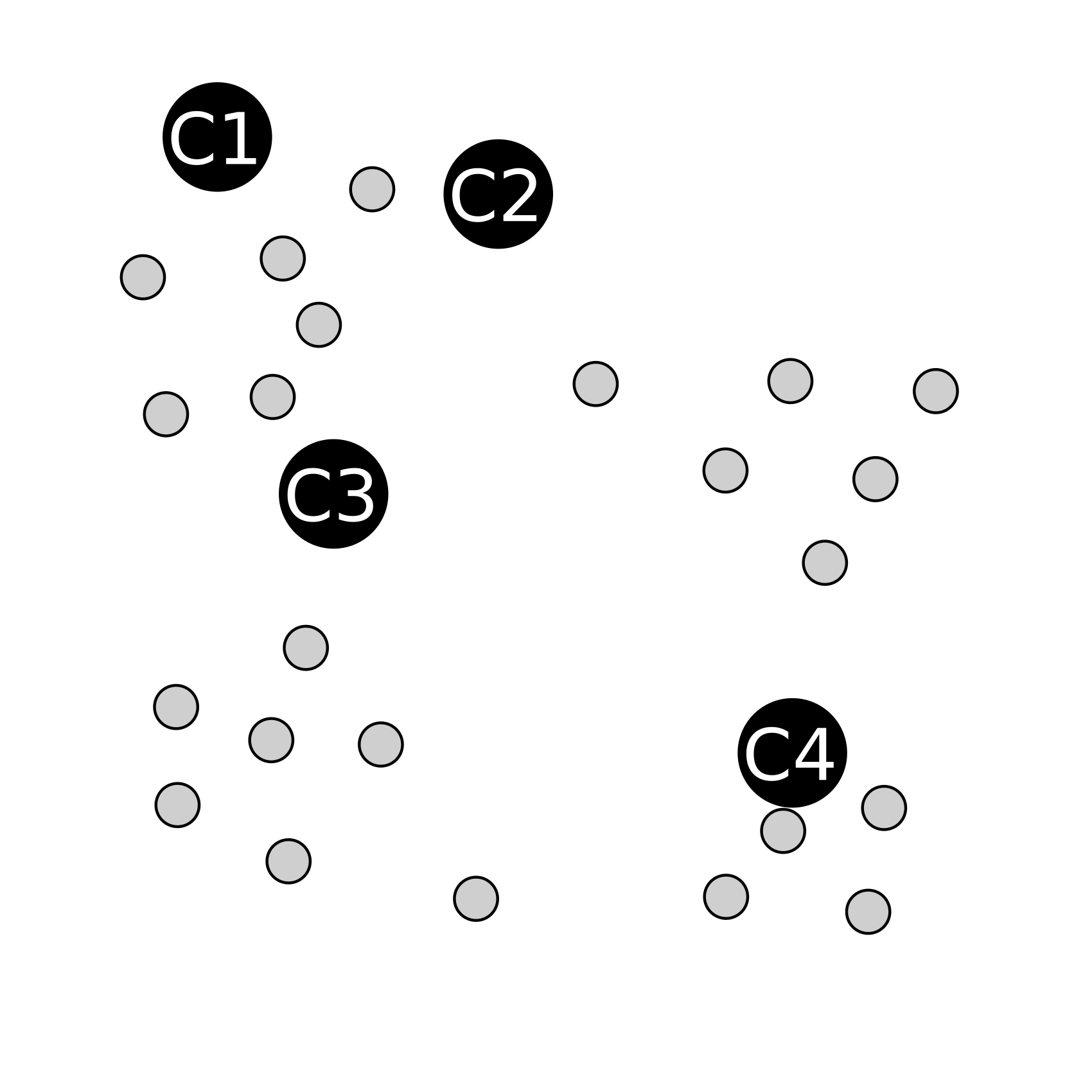
On crée des groupes de points en les "attachants" à la centroïde la plus proche (en fait il s'agit juste de mettres les points dans un même groupe, c'est l'étape d'assiignation) :

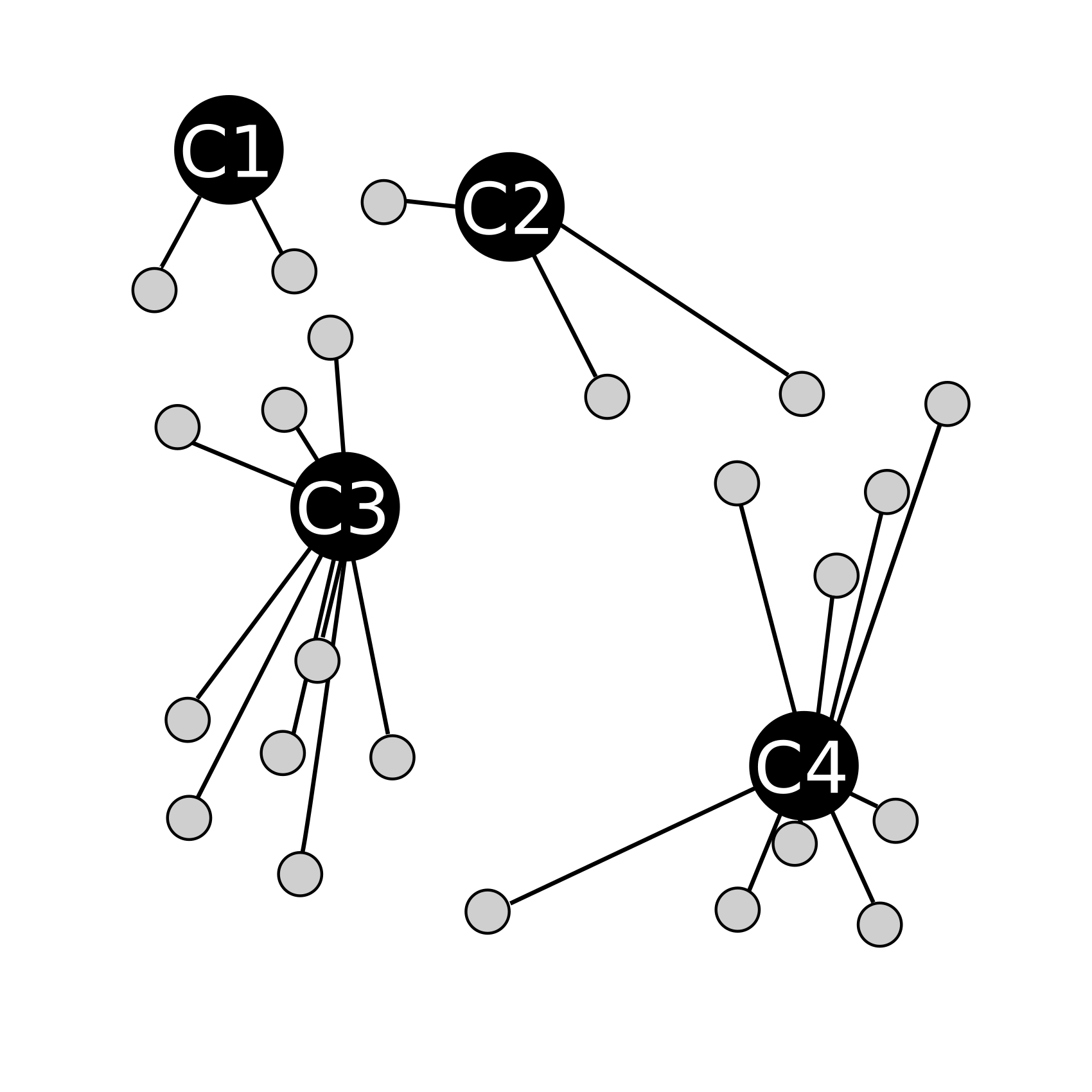
On recalcule ensuite la position des centroïdes en calculant les barycentres des groupes ainsi formés (étape de calibrage) :

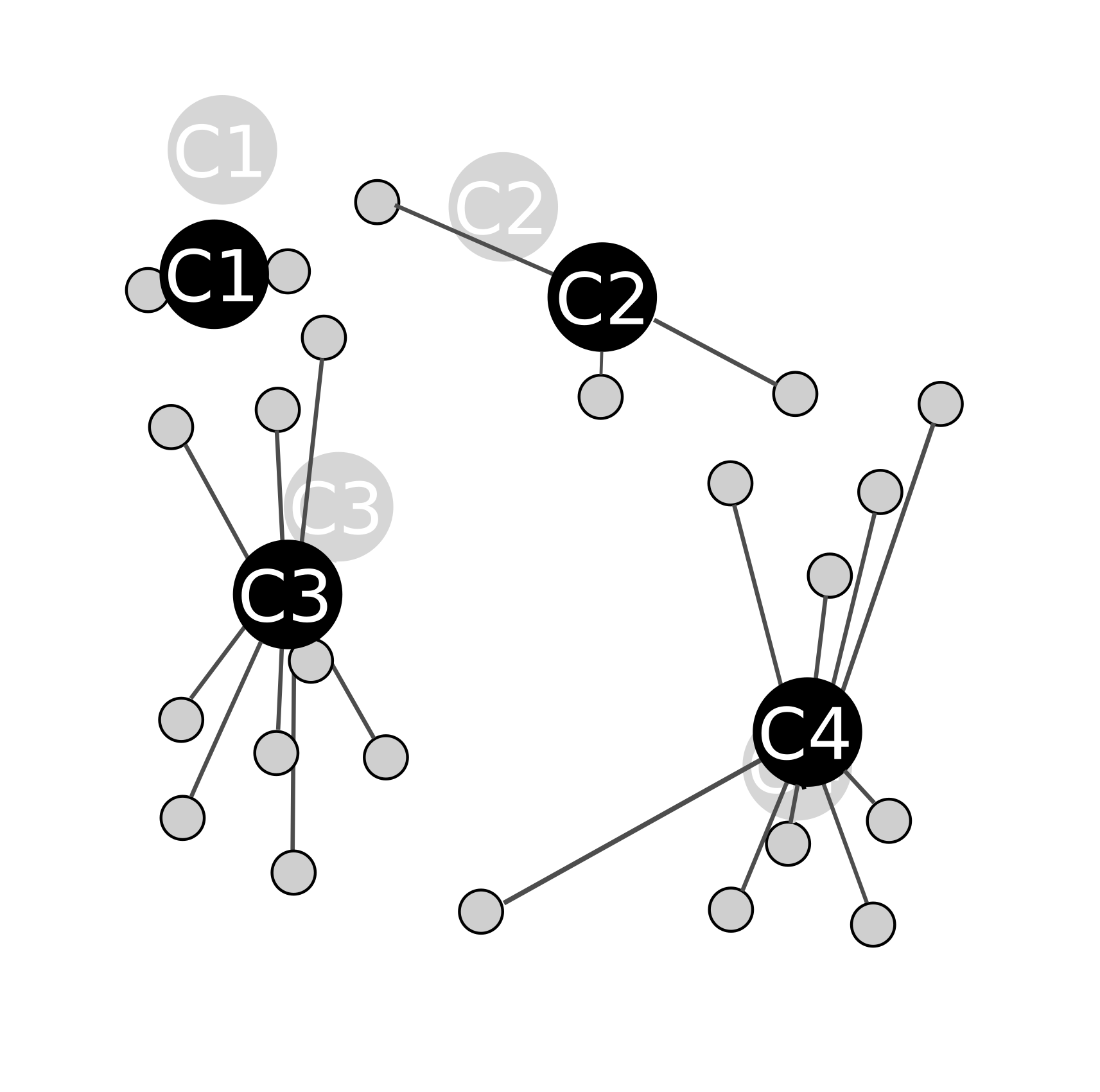
Ensuite il ne reste plus qu'à répéter les étapes d'assignation et de calibrage jusqu'à ce que les groupes ne bougent plus ; on recommence donc une assignation :

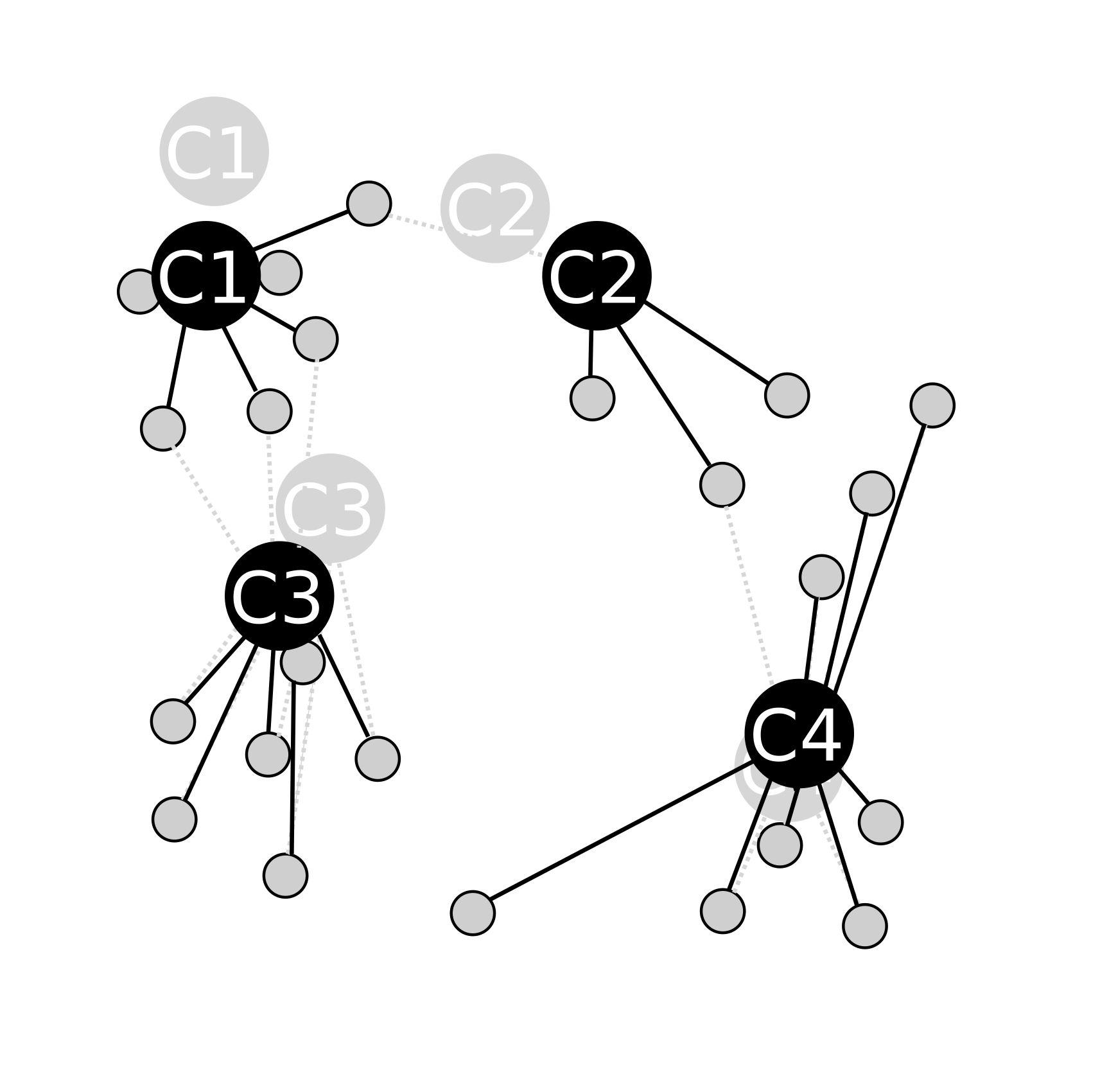
Puis un calibrage :

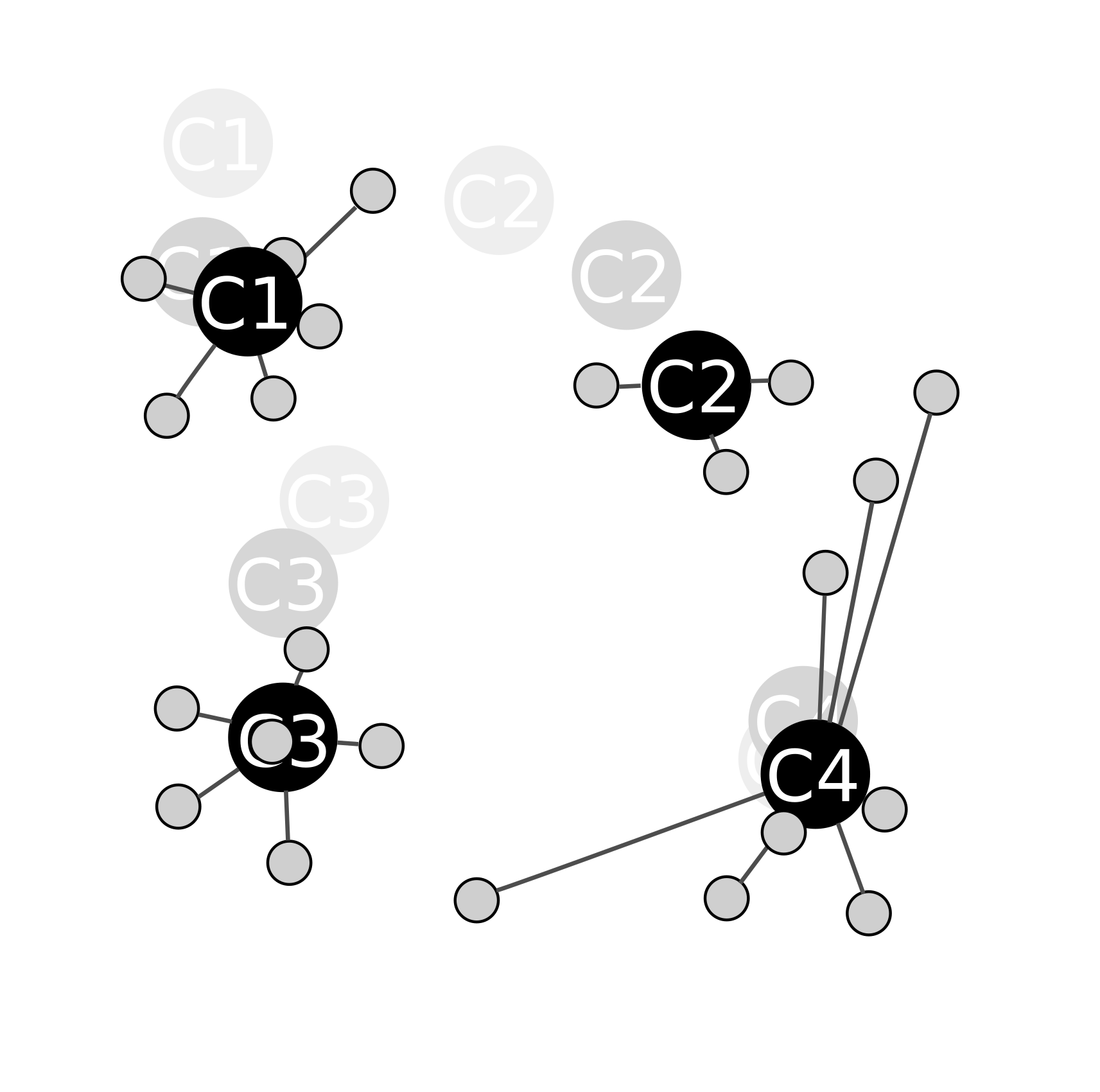
Une assignation à nouveau :

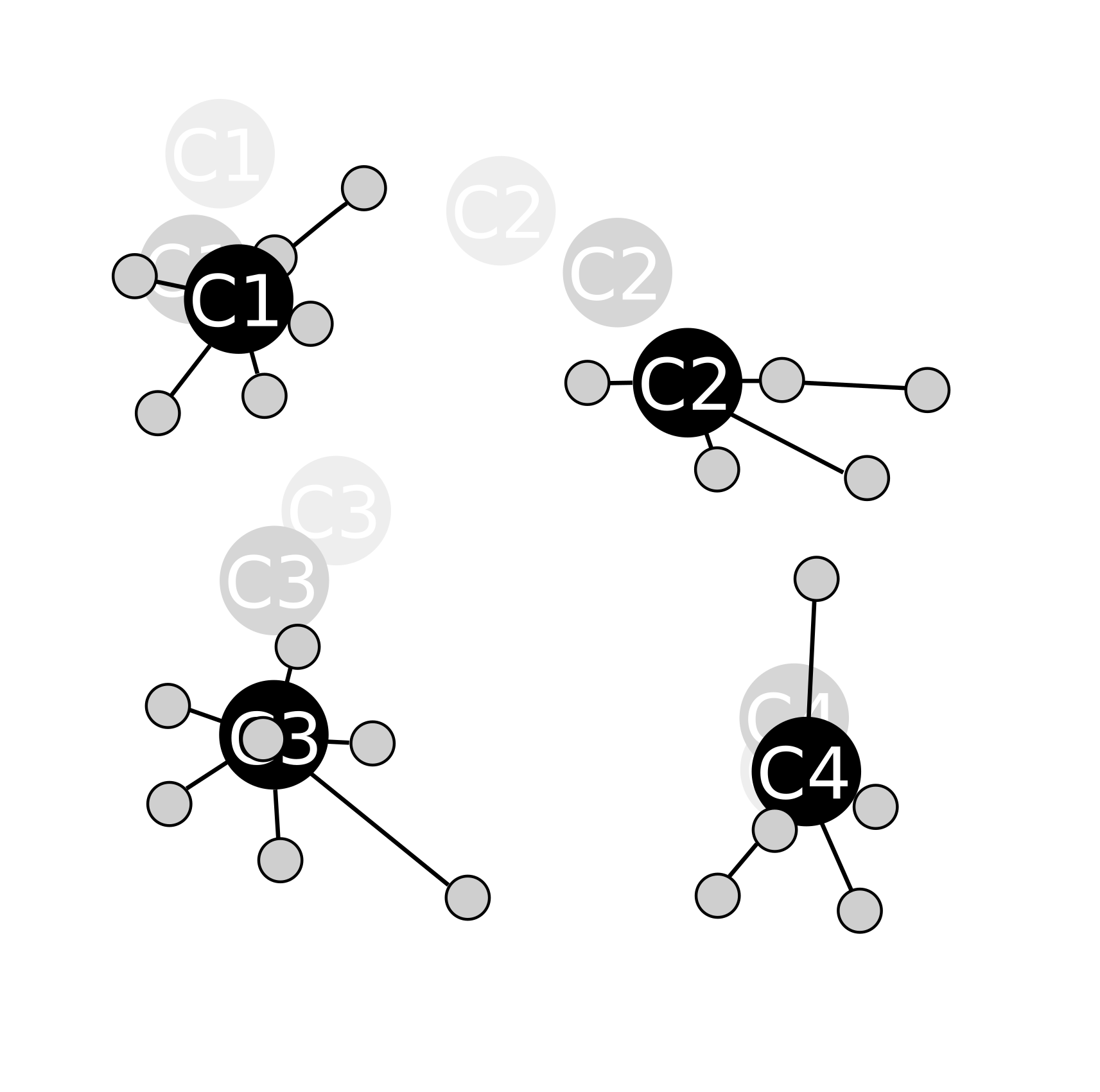
Un calibrage :

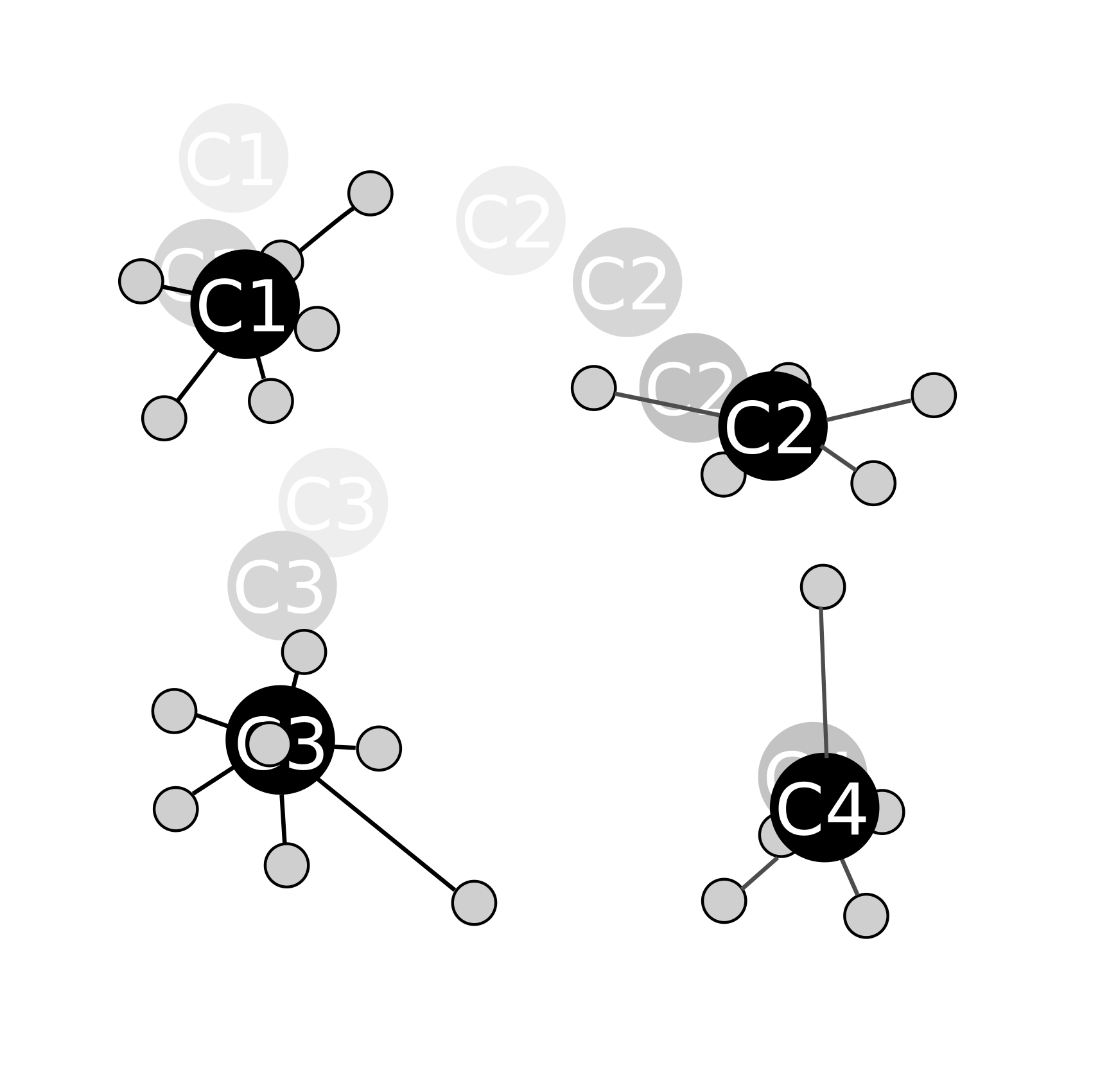
Une assignation :

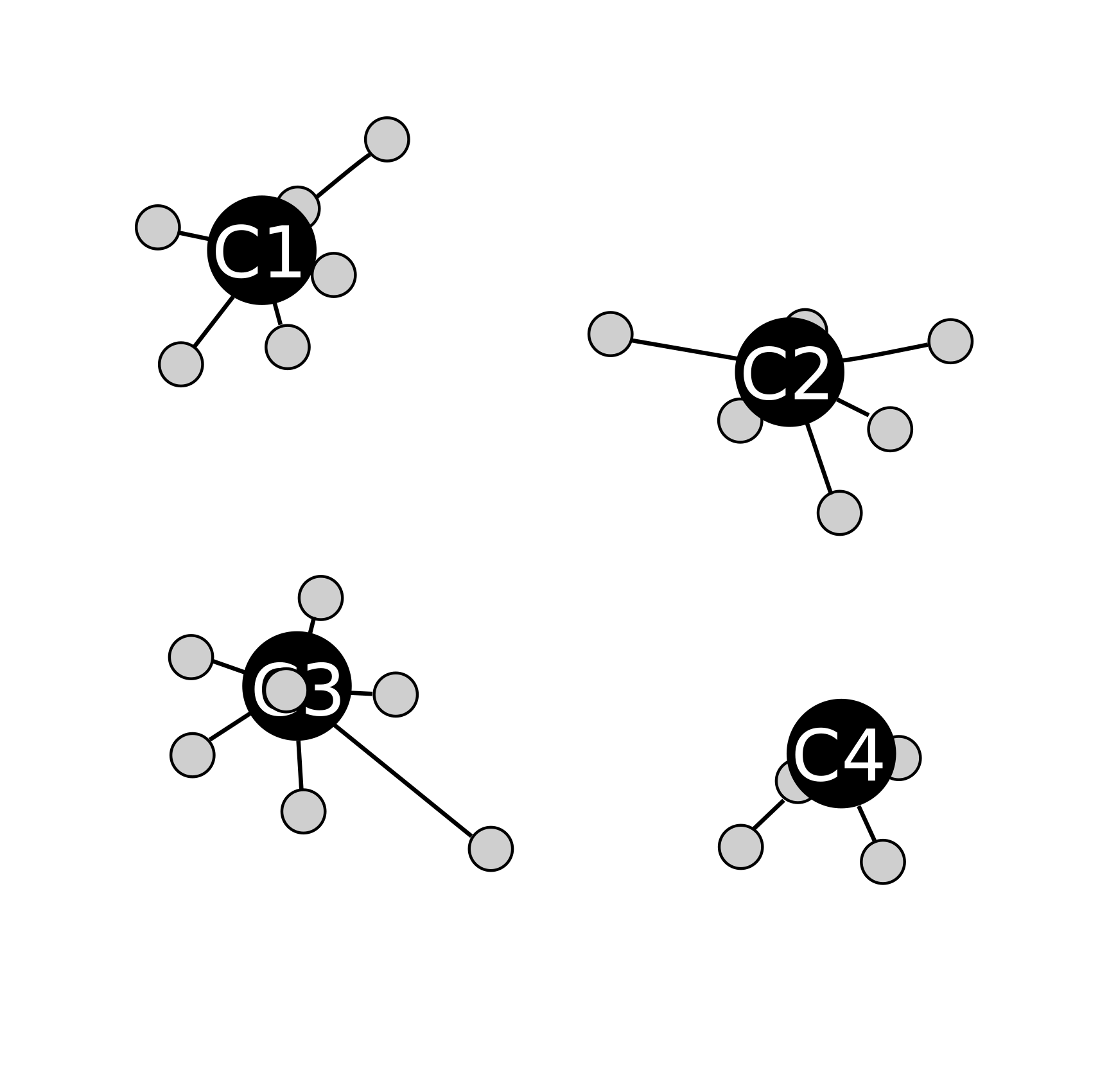
Ici, il n'y a pas besoin de refaire un calibrage car les groupes de points n'ont pas changer avec l'étape d'assignation. L'algorithme se termine en ayant automatiquement detecté les 4 groupes de point.

Exercices

Nous allons ici créer, étape par étape, un programme permettant d'exécuter l'algorithme K-means sur un nuage de points en deux dimensions. Suivez bien ces étapes et n'hésitez pas à regarder sur internet si vous vous posez des questions.

On représente ici les points par des listes de nombres.

1. Écrivez une fonction "distance" qui prend en paramètre deux points et retournent la distance entre ces deux points. On rappelle que la distance euclidienne entre deux points est définie comme suit :

   

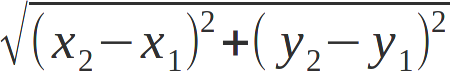
2. Copiez le code du document init.py au début de votre code pour avoir l'ensemble de points sur lequel on testera notre algorithme. Les points sont répartit en 4 groupes (g1, g2, g3, g4) mais comme nous ne sommes pas supposés connaîtres les groupes à l'avance, tous les points ont été mélangés dans une seule liste g. Tout ces points ont une abscisse et une ordonnée comprises entre 0 et 20.

   Créez une fonction init_centroides qui ne prend pas de paramètre et qui renvoie une liste de 4 centroides tirées aléatoirement (astuce : cela revient à tirer 4 fois un couple de deux nombres aléatoires). Cherchez sur internet si vous ne vous souvenez plus de comment gérer l'aléatoire en python.

3. Créez une fonction plus_proche_centroides qui prend en paramètre un point et une liste de centroides et renvoie l'index dans la liste de la centroide la plus proche du point p. Dans notre exemple avec 4 groupes, votre fonction renverra donc une valeur entre 0 et 3 inclus.

4. Créez une fonction assignation qui prend en paramètre une liste de points ainsi qu'une liste de centroides et renvoie une liste contenant les listes des différents groupes. Attention, la valeur de retour de cette fonction est bien une liste de liste de points. Dans notre exemple à 4 groupes, la fonction assignation renverra une liste contenant 4 listes contenant chacune les points associés à l'une des centroïdes.

5. Le barycentre d'un nuage de point est définit comme le point de coordonnées (m_x, m_y) où m_x est la moyennes des abscisse et où m_y est la moyenne des ordonnées des points du nuage.

   Créez une fonction barycentre qui prend en paramètre une liste de points et renvoie les coordonnées de son barycentre.

6. Créez une fonction calibrage qui prend en paramètre une liste de listes de points et renvoie une liste contenant le barycentre de chacune de ces listes de points.

7. En réutilisant les fonctions vu précédemments, créez une fonction k_means qui prend en paramètre une liste de points ainsi qu'un nombre de groupe à former et renvoie une liste de listes de points. Cette fonction va en fait renvoyer une liste contenant les points répartis dans autant de groupes que nécessaire.

8. On souhaite vérifier que les groupes ainsi formées correspondent aux groupes initiaux. Avant de lire le paragraphe suivant, prennez un instant pour réfléchir à comment cela pourrait se faire. Vous devriez assez rapidement entrevoir que ça n'est pas si évident que ça à mesurer. Il existe plusieurs méthodes, chacunes avec leurs avantages et inconvenients.

   On propose ici une méthode simpliste ; on commence par initialiser un compteur "score" à 0. Pour chaque point dans un groupe formé par l'algorithme, on regardera les points qui sont dans le même groupe : si ce point devait effectivement être dans le même groupe, on ajoute 1 au compteur score. On répète l'opération pour tous les points de tous les groupes. Implémentez la fonction score_partition qui prend en paramètre deux listes de listes de points et renvoie le score de la partition proposée par l'algorithme.

   Que est le score maximal qu'une partition peut obtenir ? Comment le calculer simplement ? Modifiez votre fonction pour qu'elle renvoie un nombre entre 0 et 1, correspondant au rapport du score obtenu par la partition sur le score maximal possible.