Bureau d'étude PEIP - IS

TP6 - Word Embeddings

Pour créer des word-embeddings, c'est à dire des vecteurs représentants le contexte de mots, on devrait utiliser un bien plus grand nombre de texte que ce qui a été fait dans le mini projet, et également opérer une réduction de dimensions sur la matrice de co-occurrence.

Il existe aussi sur internet des modèles de données pré-entrainés, qui peuvent être chargé et utilisés comme tel. Nous nous intéressons ici aux word-embeddings fournis par Word2Vec et la biblithèque gensim.

Chargement du modèle

Commençons par importer le corpus, en utilisant la sauvegarde pickle suivante : matrix_distance.pickle et matrix_sim.pickle

Pour charger une variable sauvegardée avec pickle, utilisez le code suivant :

import pickle
f = open("matrix_distance.pickle", "rb")
matrix_distance = pickle.load(f)

Travail demandé

Le but de ce TP est de construire un graphe dont les noeuds seront des mots et les arêtes des liens pondérés par la similarité (ou la distance) entre les mots. À partir de ce graphe, on essayera de déterminer les familles de mots qui sont similaires.

  1. Regardez le fichier de données words.data qui contient une trentaine de mots, et chargez la matrice 30x30 telle que, pour la i_ème ligne et j_ème colonne, la matrice contient la distance euclidienne entre le vecteur du i_ème mot du fichier et le vecteur du j_ème mot du fichier. Elle se trouve dans le fichier matrix_distance.pickle.
  2. On propose l'algorithme suivant : sachant le nombre N de familles de mots que l'on doit créer, on va enlever les arêtes du graphes les moins signiicatives jusqu'à ce que le graphe soit découpé en N composantes connexes. Cela suppose d'avoir une méthode de calcul du nombre de composante connexes d'un graphe. On propose la méthode suivante pour calculer le nombre de composantes connexes d'un graphes :
    c = 0
    Tant qu'il existe x un sommet non coloré de G:
        L = tous les voisins de x
        colorer x avec la couleur c
        Tant que L n'est pas vide :
            soit s le premier élément qu'on sorte de L
            Si s n'est pas coloré :
                colorer s avec c
                Ajouter à L tous les voisins non colorés de s
        c = c+1
    Retourner c
    Implémentez cet algorithme. Correction ici.
  3. Dans l'algorithme final décrit précédemment, que proposez vous pour "supprimer" une arête de la matrice d'adjacence ? Implémentez l'algorithme final décrit à la question précédente en faisant en sorte que celui-ci renvoie une liste de listes : celle-ci correspondra à la liste des ensembles de mots faisant partie d'une même composante connexe. Testez le pour N=3 ; observer les groupes ainsi définis.
  4. On aimerait disposer d'une méthode pour savoir à quel point les groupes ainsi définis sont correctes ou non. Dans le fichier words-gold.py sont stockées les familles de mots que nous sommes supposés trouver. On propose de calculer le score du partitionnement réalisé de la façon suivante :
    Pour chaque groupe créé :
        Calculer le % de mots de chaque famille f_i qui se trouvent dans le groupe
        Ne garder que le plus grand pourcentage pour ce groupe
    score = moyenne des % max de chaque groupe
    Implémentez cette méthode et calculer le score du partitionnement réalisé.
  5. Quel est le score du partitionnement obtenu si on utilise la similarité cosinus plutôt que la distance euclidienne ? Que faut-il changer dans les fonctions ?
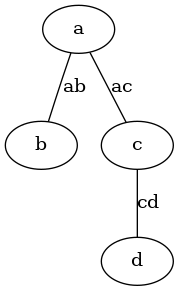
  6. On souhaite utiliser graphviz pour afficher le graphe avant et après le partitionnement, avec les valeurs des distances sur les arêtes. Voici un exemple de fichier graphviz (un fichier .dot) et le graphe qu'il génère :
    graph G {
        a -- b [label="ab"];
        a -- c [label="ac"];
        c -- d [label="cd"];
    }

    Pour générer un fichier image à partir d'un fichier .dot, on utilise la commande suivante :
    dot -Tpng mon_fichier.dot -o mon_fichier.png
    Donnez une fonction qui, à partir d'une matrice d'adjacence et de la liste des mots correspondant aux lignes et colonnes de la matrice, génère le fichier .dot correspondant en utilisant les mots comme sommets et les valeurs de similarité sur les arêtes. Afficher le graphe avant et après le partitionnement utilisant la similarité cosinus.
  7. Faire de même pour un partitionnement basé sur la distance de Levenshtein. Comparez les graphes et les scores. Lequel semble être le meilleur ? Pourquoi ?