Algorithmique - Graphes non orientés
D'après les supports de Didier Müller
Introduction
Un graphe fini G = (V,E) est défini par l’ensemble fini V ={v_1, v_2, . . . , v_n} dont les éléments sont appelés sommets (Vertices en anglais), et par l’ensemble fini E={e_1, e_2, . . . , e_m} dont les éléments sont appelés arêtes (Edges en anglais).
Une arête e de l’ensemble E est définie par une paire non ordonnée de sommets, appelés les extrémités de e. Si l’arête e relie les sommets a et b, on dira que ces sommets sont adjacents.
On appelle ordre d’un graphe le nombre de sommets n de ce graphe
Définitions
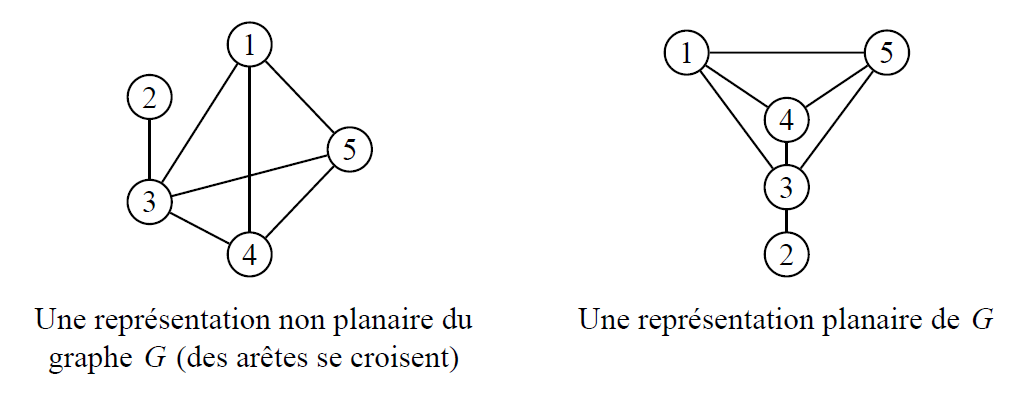
Un graphe est dit planaire si on peut le dessiner sans que deux arêtes ne se coupent. Sinon, il est dit non planaire.
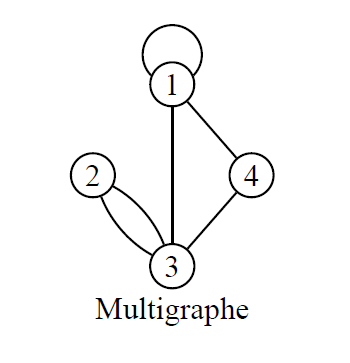
Un graphe est dit simple si au plus une arête relie deux sommets et s’il n’y a pas de boucle sur un sommet. Dans le cas contraire, on parlera de multigraphes
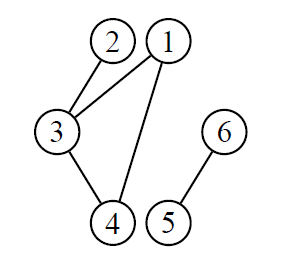
Un graphe est connexe s’il est possible, à partir de n’importe quel sommet, de rejoindre tous les autres en suivant les arêtes. Un graphe non connexe se décompose en composantes connexes. Sur le graphe ci-dessous, les composantes connexes sont {1,2,3,4} et {5,6}.
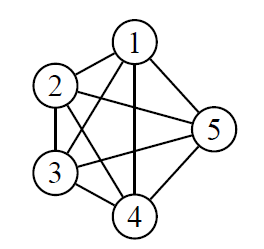
Un graphe est complet si chaque sommet du graphe est relié directement à tous les autres sommets.
Un graphe est biparti si ses sommets peuvent être divisés en deux ensembles X et Y, de sorte que toutes les arêtes du graphe relient un sommet dans X à un sommet dans Y (dans l’exemple ci-dessous, on a X = {1,3,5} et Y = {2,4}).
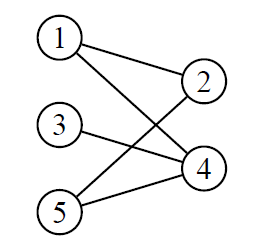
On appelle degré du sommet v, et on note d(v), le nombre d’arêtes incidentes à ce sommet. Dans un graphe simple, on peut aussi définir le degré d’un sommet comme étant le nombre de ses voisins. Attention cependant, dans un mutligraphe une boucle sur un sommet compte double.
Lemme des poignées de mains
La somme des degrés des sommets d’un graphe est égale à deux fois le nombre d’arêtes.
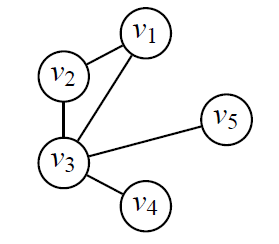
Le degré d’un graphe est le degré maximum de tous ses sommets. Dans l’exemple ci-dessous, le degré du graphe est 4, à cause du sommet v_3
Chaînes et cycles
Une chaîne dans G, est une suite ayant pour éléments alternativement des sommets et des arêtes, commençant et se terminant par un sommet, et telle que chaque arête est encadrée par ses extrémités.
On dira que la chaîne relie le premier sommet de la suite au dernier sommet. En plus, on dira que la chaîne a pour longueur le nombre d’arêtes de la chaîne.
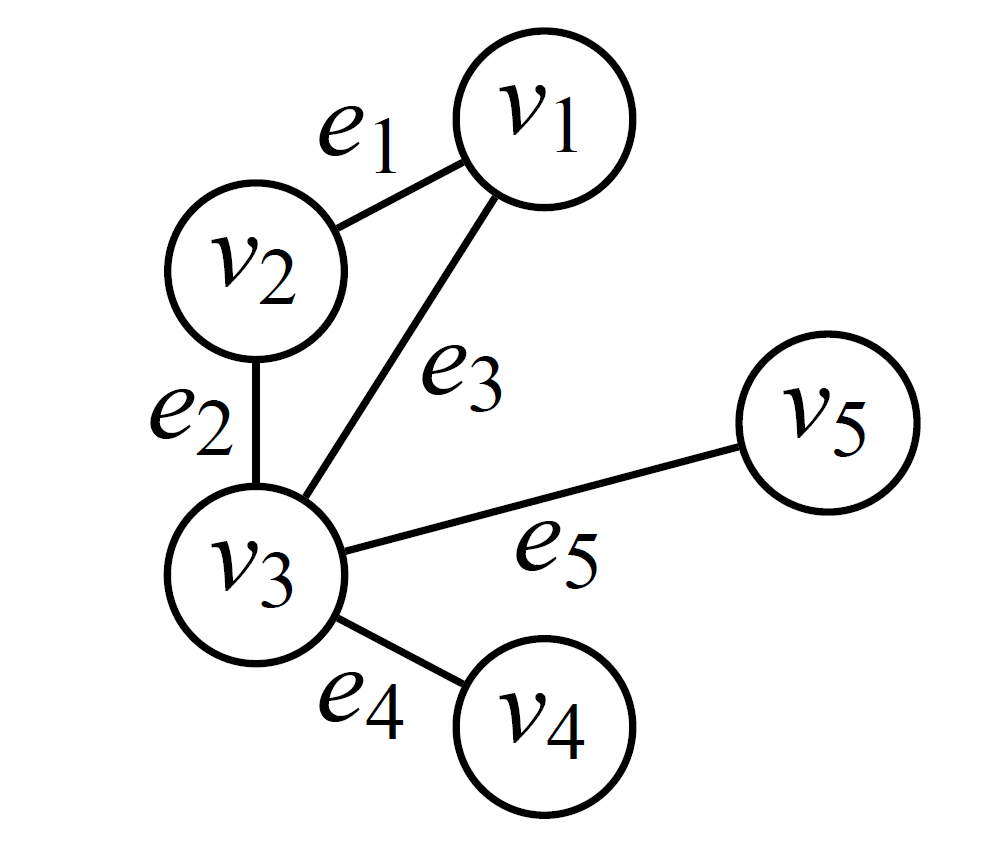
Le graphe ci-dessous contient entre autres les chaînes (v_1, e_1, v_2, e_2, v_3, e_5, v_5) et (v_4, e_4, v_3, e_2, v_2, e_1, v_1).
Quelques définitions :
- - On appelle distance entre deux sommets la longueur de la plus petite chaîne les reliant.
- - On appelle diamètre d’un graphe la plus longue des distances entre deux sommets.
- - Une chaîne est élémentaire si chaque sommet y apparaît au plus une fois.
- - Une chaîne est simple si chaque arête apparaît au plus une fois.
- - Une chaîne fermée (dont les sommets de départ et de fin sont identiques) et simple est appelée cycle.
Théorème
Pour un graphe G ayant m arêtes, n sommets et p composantes connexes, on définit v(G) (qu'on prononce 'nu de G'):
v(G) = m − n + p
v(G) est appelé le nombre cyclomatique de G. On a v(G) ≥ 0 pour tout graphe G, et v(G)=0 si et seulement si G est sans cycle.
Graphes partiels et sous graphes
Soit G = (V,E) un graphe. Le graphe G' = (V,E') est un graphe partiel de G, si E' est inclus dans E . Autrement dit, on obtient G' en enlevant une ou plusieurs arêtes au graphe G.
Pour un sous-ensemble de sommets A inclus dans V , le sous-graphe de G induit par A est le graphe G' = (A,E(A) dont l’ensemble des sommets est A et l’ensemble des arêtes E(A) est formé de toutes les arêtes de G ayant leurs deux extrémités dans A. Autrement dit, on obtient G' en enlevant un ou plusieurs sommets au graphe G, ainsi que toutes les arêtes incidentes à ces sommets.
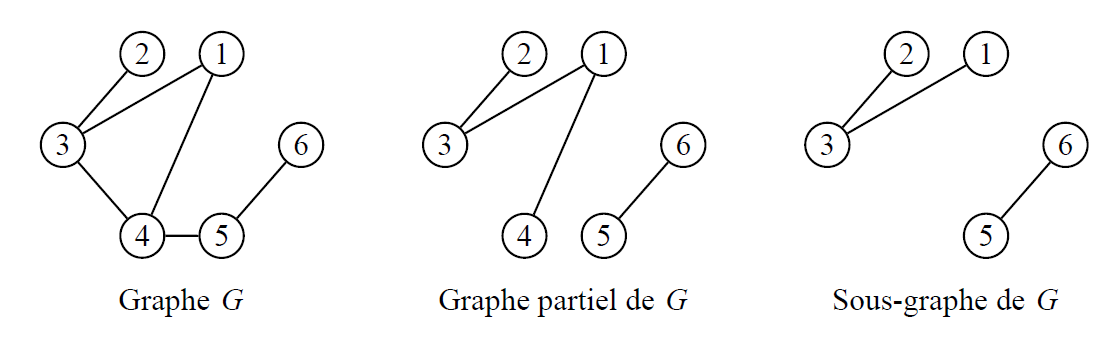
On appelle clique un sous graphe complet de G
Graphes Eulériens
On appelle cycle eulérien d’un graphe G un cycle passant une et une seule fois par chacune des arêtes de G. Un graphe est dit eulérien s’il possède un cycle eulérien.
On appelle chaîne eulérienne d’un graphe G une chaîne passant une et une seule fois par chacune des arêtes de G. Un graphe ne possédant que des chaînes eulériennes est semieulérien.
Plus simplement, on peut dire qu’un graphe est eulérien (ou semi-eulérien) s’il est possible de dessiner le graphe sans lever le crayon et sans passer deux fois sur la même arête.
Graphes Hamiltonien
On appelle cycle hamiltonien d’un graphe G un cycle passant une et une seule fois par chacun des sommets de G. Un graphe est dit hamiltonien s’il possède un cycle hamiltonien.
On appelle chaîne hamiltonienne d’un graphe G une chaîne passant une et une seule fois par chacun des sommets de G. Un graphe ne possédant que des chaînes hamiltoniennes est semi-hamiltonien.